2018考研数学高数考点解析一:函数极限连续、微分
分享至好友和朋友圈
高等数学作为硕士研究生招生考试的内容之一,主要考查考生对高等数学的基本概念、基本理论、基本方法的理解和掌握以及考生的抽象思维能力、逻辑推理能力、综合运用能力和解决实际问题的能力。
依据数学考试大纲中的考试要求,跨考教育数学教研室包新卓老师在下面的表格中简要罗列了高等数学在数学(一)、数学(二)和数学(三)这三个卷种中所涵盖的考试内容。
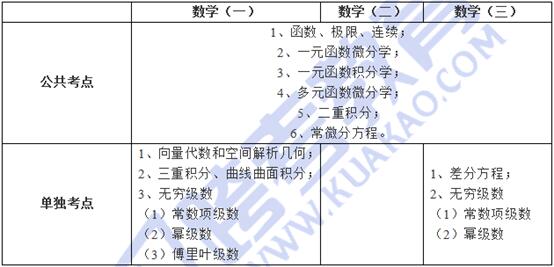
接下来,跨考教育包新卓老师就从数学(一)、数学(二)、数学(三)的公共部分开始。
一、函数、极限、连续
高等数学在考研中,也被称为微积分学。微积分学的研究对象是函数,许多重要的概念都需要用极限理论精确定义,因此极限是微积分学的重要基础,这部分内容对后续内容的学习影响深远,故应重点掌握。
在这一部分,由于数学(一)、数学(二)、数学(三)的考试要求完全一样,故这里不做分类。
考纲内容:
1、函数的概念及表示法、函数关系的建立;
2、函数的有界性、单调性、周期性和奇偶性;
3、复合函数、反函数、分段函数和隐函数;
4、基本初等函数的性质及其图形,初等函数;
5、数列极限与函数极限的定义及其性质;
6、函数的左极限和右极限;
7、无穷小量和无穷大量的概念及其关系,无穷小量的性质及无穷大量的比较;
8、极限的四则运算:掌握极限的四则运算法则;
9、极限存在的两个准则(单调有界准则和夹逼准则),两个重要极限;
10、函数连续的概念,函数间断点的类型;
11、初等函数的连续性,闭区间上连续函数的性质;
根据往年改卷反馈回来的数据可知,大部分考生对函数、极限、连续这一部分的内容普遍掌握得比较好,但由于这部分内容与后续内容多有交叉,因此考生要注意前后知识的融会贯通。
二、一元函数微分学
一元函数微分学不仅在微积分的学习中占有着极其重要的地位,而且它也是考研数学考查的重点。在这里,对于数学(一)和数学(二)单独考点,跨考教育包新卓老师会在相应的内容后面予以标出,未做任何标出的内容则为数学(一)、数学(二)、数学(三)的公共考点。
(一)考纲内容:
1、导数和微分的概念:须掌握一阶导数和二阶导数的定义式;
2、导数的意义:
(1)几何意义:
(2)物理意义:数学(一)、(二);
(3)经济意义:数学(三);
3、函数的可导性与连续性之间的关系;
4、导数和微分的四则运算;
5、基本初等函数的导数、复合函数、反函数、隐函数以及参数方程所确定的函数的微分法,高阶导数,一阶微分形式的不变性;
6、微分中值定理;
7、导数的应用,具体考点如下:
(1)平面曲线的切线和法线;
(2)洛必达法则;
(3)函数单调性的判别;
(4)函数的极值;
(5)函数图形的凹凸性、拐点及渐近线;
(6)函数图形的描绘;
(7)函数的最大值与最小值;
(8)弧微分、曲率的概念、曲率圆与曲率半径:数学(一)、(二)。
(二)重点及常见考点:
1、基本概念方面:重点有导数和微分的定义、可导与连续的关系。考生需要掌握一阶和二阶导数的定义,会利用导数的定义讨论分段函数在分段点处的可导性。
2、理论方面:重点是罗尔定理,拉格朗日中值定理,柯西中值定理;这里考生要掌握通过构造辅助函数证明中值问题。
3、计算方面:重点是基本初等函数的导数、微分公式,导数、微分的四则运算以及反函数、隐函数和由参数方程确定的函数的求导公式。此外,这里还要求考生会求函数的二阶导数和某些函数的n阶导数。
4、应用部分:重点是利用导数研究函数的性态。
 京公网安备11010202009747号
京公网安备11010202009747号